TRANSVERSE STABILITY, SMALL ANGLES
So far, consideration has been given only to a ship when in equilibrium or moving slowly from one position of equilibrium to another. Now consider what happens when a ship is subject to a small heeling moment.
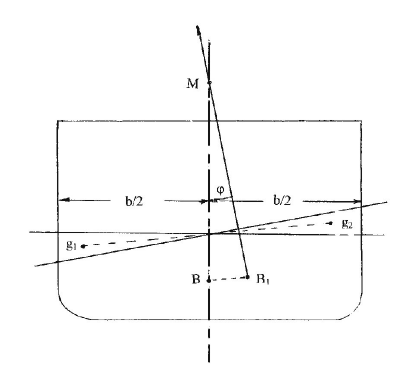
For small disturbances, it is reasonable to assume that there is no change in trim and that the upright and heeled waterlines will intersect on the centreline of the ship. The ship will take up a small angle of heel.

There will be a newly submerged wedge of hull on one side of the centreline and a corresponding emerged wedge on the other. The centre of buoyancy will move from its initial position in the centreline plane, B, to a new position B1 such that the distance between the two positions represents the moment of transfer of buoyancy between the two wedges. The line BB1 will be parallel to the line joining the centres of volume of the two wedges.
The total buoyancy force remains constant but it now acts in a vertical line through B1, that is normal to the inclined waterline. This line intersects the ship’s centreline plane in M, the metacentre. As previously noted, M can be taken as a fixed point for small angles, typically up to about 10 degrees.
The weight W (equal to the buoyancy) will act through the centre of gravity of the ship which remains fixed. The resultant moment acting on the ship will be given by:
W.GM.ϕ where ϕ is the angle of heel, assumed small
From a stability point of view, there are three possibilities:
• M is above G. In this case, the moment acting, due to the shift in buoyancy, is tending to restore the ship to the upright position. The ship is said to be stable; it has positive stability.
• M is below G. In this case, the moment is trying to push the ship further from the upright. The ship is said to be unstable; it has negative stability.
• M and G coincide. In this case, there is no moment acting on the ship which will remain in the heeled position. The ship is said to have neutral stability.
The vertical distance between the centre of buoyancy and the metacentre is given by:
BM = I/V, where I is the second moment of area, or the inertia, of the waterplane about a longitudinal axis and V is the total volume of displacement.
For a rectangular waterplane of length, L, and breadth, B, the inertias about its centreline are given by:
I = B3L/12
In general terms, V will be proportional to LBT where T is the draught of the vessel concerned.
Thus, in this case, BM = Const.B3/T
Although a normal ship’s waterplane is not rectangular, this general relationship will be approximately true for ships. Thus, the beam has a very great influence on the initial stability of a ship. It might appear, at first, that good stability could be obtained by making the draught small. Whilst true for small angles, the stability at large angles would suffer.
It has been seen that the positions of points B and M depend only upon the geometry of the ship and are fixed for the draught at which it is floating. G depends upon the loading condition of the ship and will vary with time. With the metacentric diagram, a master can find M for the draught at which the ship is floating. From the loading of the ship, the master will be able to assess the position of G. The value of GM, and hence the initial stability follows.