Ship Stability – Movement of the Centre of Gravity
Centre of gravity
It is the point of a body at which all the mass of the body may be assumed to be concentrated.
The force of gravity acts vertically downwards from this point with a force equal to the weight of the body.
Basically the body would balance around this point.
The COG of a homogeneous body is at its geometrical centre.
Effect of removing or discharging mass


Consider a rectangular plank as shown. The effects of adding or removing weights would be as shown:
Now cut the length of plank of mass ‘w’ kg whose CG is ‘d’ mtrs away from CG of the plank.
Note that a resultant moment of ‘w x d’ kg m has been created in an anti-clockwise direction about ‘G’.
The CG of the new plank shifts from ‘G’ to ‘G1’.
The new mass (W-w) kg now creates a tilting moment of (W-w) x GG1 about G.
Since both are referring to the same moment,
(W-w) x GG1 = w x d
GG1 = (w x d)/(W-w)
CONCLUSION: When a weight is removed from a body, the CG shifts directly away from the CG of the mass removed, and the distance it moves is given by:
GG1 = (w x d)/Final mass metres
Where, GG1 is the shift of CG
w is the mass removed
d is the distance between the CG of the mass removed and the CG of the body.
Effect of adding or loading mass
Equating the tilting moments created due to the added weight, which must again be equal:
(W + w) x GG1 = w x d
GG1 = (w x d)/(W + w)
GG1 = (w x d)/ (Final mass) metres
Application to ships
DISCHARGING WEIGHTS:
GG1 = (w x d) / (Final displacement) metres
LOADING WEIGHTS
GG1 = (w x d) / (Final displacement) metres
Shifting Weights
GG2 = (w x d) / (Displacement) metres
Vertical Weight Shifts
Shifting weight vertically, no matter where onboard it is, will always cause the ship’s center of gravity to move in the same direction as the weight shift.

To calculate the height of the ship’s center of gravity after a vertical weight shift, the following equation is used:
KG1 = ((W0 x KG0) +/- (w x kg)) / ΔF
KGO = The original height of the ship’s center of gravity (M)
Δo = The ship’s displacement prior to shifting weight (MT)
w = The amount of weight shifted (MT)
kg = The vertical distance the weight was shifted (M)
ΔF = The ship’s displacement after shifting the weight (MT)
(+) When the weight is shifted up use (+)
(-) When the weight is shifted down use (-)
Example Problem
10 MT of cargo is shifted up 3 M. ΔO is 3500 MT and KGo is 6 M. What is the new height of the ship’s center of gravity (KG1)?
KG1 = ((Δo x KGo) +/- (w x kg)) / ΔF
KG1 = ((3500 x 6) + (10 x 3)) / 3500
KG1 = 6.009 M
Vertical Weight Additions/Removals
When weight is added or removed to/from a ship, the vertical shift in the center of gravity is found using the same equation.
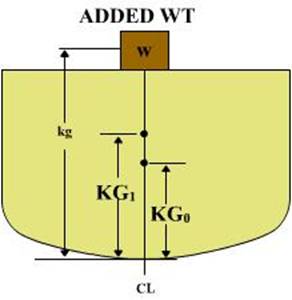
KG1 = ((Δo x KGo) +/- (w x kg)) / ΔF
KGO = The original height of the ship’s center of gravity (M)
ΔO = Ship’s displacement prior to adding/removing weight (MT)
w = The amount of weight added or removed (MT)
kg = The height of the center of gravity of the added/removed weight above the keel (M)
ΔF = The ship’s displacement after adding/removing the weight
(+) When the weight is added use (+)
(-) When the weight is removed use (-)
Example Problem
A 30 MT crate is added 10 M above the keel. Δo is 3500 MT and KG0 is 6 M. What is the new height of the ship’s center of gravity (KG1)?
KG1 = ((Δo x KGo) +/- (w x kg)) / ΔF
KG1 = ((3500 x 6) + (30 x 10)) / 3530
KG1 = 6.034 M
Horizontal Weight Shifts
Shifting weight horizontally, no matter where onboard it is, will always cause the ship’s center of gravity to move in the same direction as the weight shift.
NOTE: A weight shift causing the ship’s center of gravity to move off centerline will always reduce the stability of the ship.

To calculate the horizontal movement of the ship’s center of gravity, the following equation is used:
GG2 = (w x d) / ΔF
w = The amount of weight shifted (MT)
d = The horizontal distance the weight is shifted (M)
ΔF = The ship’s displacement after the weight is shifted (MT)
Example Problem
A 50 MT weight is shifted 10 M to starboard. ΔO is 32000 MT.
What is the change in the center of gravity (GG2)?
GG2 = (w x d) / ΔF
GG2 = (50 x 10) / 32000
GG2 = 0.01562 M
Horizontal Weight Additions/Removals
When an off-center weight is added or removed to/from a ship, the ship’s center of gravity will move off centerline, the ship will develop a list.

To calculate the horizontal movement of the ship’s center of gravity after adding/removing an off-center weight, the same equation is used:
GG2 = (w x d) / ΔF
w = The amount of weight added/removed (MT)
d = The distance from the center of gravity of the weight to the ship’s centerline (M)
ΔF = the ship’s displacement after the weight is shifted (MT)
Example Problem
50 MT of cargo is loaded onto the Tween deck, 10 M from centerline. ΔO is 48000 MT. What is the change in the center of gravity (GG2)?
GG2 = (w x d) / ΔF
GG2 = (50 x 10) / 48000
GG2 = 0.0104 M
Effect of suspended weights
The CG of a body is the point through which the force of gravity may be considered to act vertically downwards.
For a suspended weight, whether the vessel is upright or inclined, the point through which the force a gravity may be considered to act vertically downwards is g1, the POINT OF SUSPENSION.




Conclusions
The CG of a body will move directly TOWARDS the CG of any weight ADDED.
The CG of a body will move directly AWAY from the CG of any weight DISCHARGED.
The CG of a body will move PARALLEL to the shift of the CG of any weight MOVED within the body.
The shift of the CG of the body in each case is given by the following formula:
GG1 = w x d / W metres
where w = weight added, removed or shifted.
W = final mass of the body
d = distance between the CG if weight added or removed, or the distance by which the weight is shifted.
When a weight is SUSPENDED, its CG is considered to be at the POINT OF SUSPENSION.
Written by Capt. Jayant Roy





